May 2015 – EEPP Scrapbook

The following are the numerical answers to the questions on the 7-5-2015 tutorial sheet.

I wrote a MATLAB/Octave script to check my answers. In case you want to take a look at it (for example if you’re trying to work out why one of my answers is different from yours), you can download it here.

Q1.

The time constant τ = 0.1 s

Q2.

The time constant τ = 0.0001 s = 100 μs

Q3.

The time constant τ = 0.001 s = 1 ms

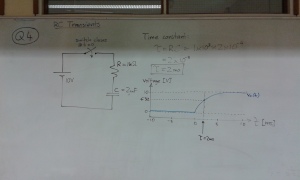
Q4.

v_C(0.002) = 6.32 V.

Q5.

The time constant τ = 1 s.
v_C(τ) = 4.4146 V.

Q6.

2 true nodes
1 binary nodes
3 branches
Vs and R1 are in series
R2 and R3 are in parallel

Q7.

4 true nodes
3 binary nodes
6 branches
V2, V1 and R1 are in series
R4 and R6 are in series
No elements are in parallel

Q8.

4 true nodes
3 binary nodes
6 branches
Vs and R1 are in series
C1, R4 and R5 are in series
No elements are in parallel

Q9.

5 true nodes
1 binary node
8 branches
R6 and R7 are in series
No elements are in parallel

Q10.

2 true nodes
2 binary nodes
4 branches
Vs and R1 are in series
R4 and R5 are in series
R2 and R3 are in parallel

Q11.

I₁ = 0.01125 A = 11.25 mA
I₂ = 0.00375 A = 3.75 mA

Q12.

I₁ = 0.1 A = 100 mA
V₁ = 2.5 V

Q13.

I₁ = 0.00555 A = 5.55 mA
I₂ = 0.00111 A = 1.11 mA

Q14.

I₁ = 0.41143 A = 411.43 mA
I₂ = 0.13714 A = 137.14 mA

Q15. (DC circuit analysis)

I = 0.02857 A = 28.57 mA

Q16. (DC circuit analysis)

I₁ = 0.1 A = 100 mA
I₂ = 0.03333 A = 33.33 mA

Q15. (phasors)

|V| = 230.71 V
Φ = angle(V) = 1.049 rad = 60.101°

In polar form, V = 230.71 ∠60.101°

A mathematical expression for v(t):

$v(t) = V_{pk} \cos\left( \omega t + \Phi \right) \textrm{ [V]}$

where

$\omega = 2 \pi f = 100 \pi \textrm{ rad/s}$
$\Phi = 1.049 \textrm{ rad}$
$V_{pk} = \sqrt{2}\times V_{rms} = \sqrt{2}\times 230.71 = 326.27 \textrm{ V}$

Hence,

$v(t) = 326.27 \cos\left( 100\pi t + 1.049 \right) \textrm{ [V]}$

Q16. (phasors)

V_C = 5.0 ∠-0.6435 rad

Q17.

The phase difference between V_R and V_C is 1.3455 rad.
V_R leads V_C.

Mathematical expressions for V_R and V_C:

$v_R(t) = 141.42 \cos\left( 100\pi t + 0.92730 \right) \textrm{ [V]}$
$v_C(t) = 278.57 \cos\left( 100\pi t - 0.41822 \right) \textrm{ [V]}$

Q18.

I_S = 0.23 – 0.00004817j [A]
V_L = 0.000010089 + 0.048171j [V]

Q19.

I_S = 0.0067777 – 0.0046444j [A]

Q20.

V₁ = 0.073898 + 0.392176j [V]

Q21.

V_L = 2.2779 + 5.3051j [V]

During yesterday’s tutorial, I did my best to snap a picture each time I was about to wipe the whiteboard. I probably didn’t capture everything, but if you couldn’t make it to the tutorial, the following photos will give you a general idea about what we covered:

Tips on RLC / impedance circuit analysis

NOTE: In question 17 on phasors, I forgot to mention in the question that the frequency is 50 Hz. You need to know the frequency to write the mathematical expressions for vr(t) and vc(t).

I also just noticed that I mixed up the numbering when I was writing out the tutorial questions. I accidentally numbered two questions as Q15 and two questions as Q16. The first Q15 and Q16 are on DC circuit analysis. The second Q15 and Q16 are on phasors. The Q15 in the whiteboard photos above is the one on phasors.

Month: May 2015

Answers to questions on the 7-5-2015 tutorial sheet

Whiteboard photos from pre-exam tutorial 8-5-2015